研究の背景
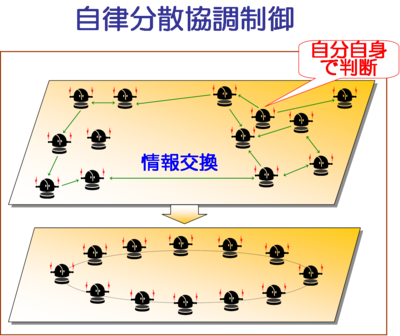
ネットワーク技術の進歩により,工学の扱うべき対象は急速に大規模・複雑化 してきている.それに対応すべく様々な分野において,異なるアプローチでの 研究が盛んに行われてきている.その中の大きな流れの一つは,マルチエージェント システムの自律分散制御である(例えば、Olfati-Saber et.al., 2007). 具体的応用例としては,複数のロボットによる協調制御・フォーメーション制御や 空間的に分布している複数のセンサによる分散予測など工学的問題ばかりでなく, 遺伝子制御ネットワークなど生命現象の解明や気象など大規模な自然現象の解明や 制御なども、この枠組みで捉えることができる.
しかし,これまでの研究の多くは個別の問題設定に対する個別手法の提案という 形のものが多く,統一的な理論体系化への方向性が見えていないのが現状である. そこで本研究では,大規模な動的システムを解析・設計するための統一的な 枠組みの一つとして「一般化周波数変数を持つ線形システム」を提案し, システム制御論としての展開を図る.
研究の着眼点と目的
本研究では,均質な動的マルチエージェントシステムを対象とする.すなわち, 複数の同一のエージェント(動的システム)が相互に情報交換を行うことに より協調してある与えられた機能を実現するシステムを考える. このようなシステムは,各エージェントの動的挙動を表す伝達関数を h(s) と し,エージェントの個数を n とすると,h(s)I_n を定数行列で結合 (線形分数変換の形で)したシステムとして表現できる.
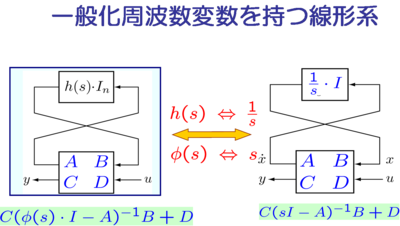
これは,通常の連続時間系における周波数変数 s を φ(s):=1/h(s) で 置き換えた形式と全く同じである.そこで,ある伝達関数 G(s) の変数 s を有理関数 φ(s) で置き換えて得られるシステム G(φ(s)) のことを 「一般化周波数変数を持つ線形システム」と呼び,このようなクラスの システムに対するシステム制御論を展開していく.具体的には,基礎的事項 である可制御性・可観測性,安定性から始まり,H2ノルムやH∞ノルムなど 性能評価の計算法を検討する.最終的にはは,導かれた解析結果に 基づいて,設計問題に対する答え(マルチエージェントシステムに対する 系統的設計手法)を与えることを目的とする.
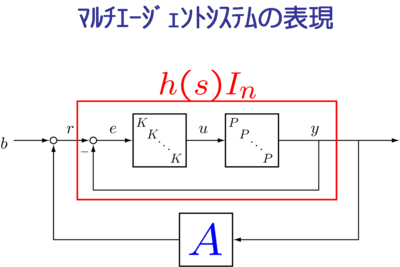
一般化周波数変数を持つ線形システムの表現
一般化周波数変数を持つ線形システムは,通常のシステム
G(s) = C (sI_n-A)^{-1} B + D
の周波数変数 s を φ(s):=1/h(s) で置き換えた形式
G(φ(s)) = C (φ(s)I_n-A)^{-1} B + D
で与えられる.
一般化周波数変数を持つ線形システムの可制御性・可観測性
いま,h(s) の状態空間実現が (A_h, b_h, c_h, 0) で
与えられているとすると,G(φ(s)) の状態空間実現 (Aφ, Bφ, Cφ, Dφ) は
Aφ = I_n \otimes A_h + A \otimes (b_h c_h) ,Bφ = B \otimes b_h
Cφ = C \otimes c_h , Dφ = D
と書ける.この実現に基づいて可制御性・可観測性に関する解析が可能で,
以下の定理が成り立つ.
(A_h, b_h, c_h, 0) をh(s) の最小実現とし,(A, B, C, D) が 可制御性かつ可観測性であると仮定する.このとき,G(φ(s)) の状態空間 実現 (Aφ, Bφ, Cφ, Dφ) は 可制御性かつ可観測性である.
すなわち,通常の直列接続や並列接続の場合と異なり,2つのシステムの間の 極・零点相殺を考慮する必要はない.
一般化周波数変数を持つ線形システムの安定性
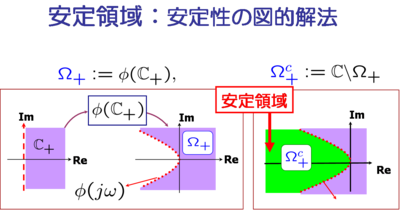
可制御性・可観測性の結果は,G(φ(s)) の安定性と(φ(s)I_n-A)^{-1} の安定性と が等価であることを示している.この事実を利用すると, h(s) の多項式規約分解が h(s)=n(s)/d(s) で与えられるとき, G(φ(s)) が安定であるための必要十分条件は以下で与えられる. 「A の任意の固有値は,p(λ,s) := d(s) - λn(s) が Hurwitz となる複素数λの 集合の要素である.」すなわち,A の固有値の存在条件が複素平面で与えられる (下図を参照).
一般化周波数変数を持つ線形システムの安定判別法
上記の安定条件に,複素係数を持つ多項式の Hurwitz タイプの安定判別法 (Frank, 1946)と一般化リアプノフ安定条件(Hinrichsen and Pritchard : Mathematical Systems Theory I, 2004)を適切に組み合わせて適用することにより, n 個の独立な線形行列不等式(LMI)条件で構成される安定条件(必要十分条件)を 系統的に求めることができる.例えば,h(s) = (cs+d)/(s^2+as+b) で与えられる 2次の h(s) に対する安定条件は,以下で与えられる.

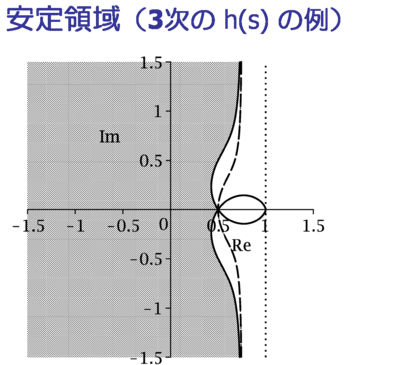
安定判別法:3次の h(s)
h(s) = (2s^2+s+1)/(s^3+2s^2+s+1) で与えられる3次の h(s) に対して, 安定条件を満たすために行列 A の固有値が存在すべき領域を求めると, 下図のハッチを施した部分与えられる.この図で,点線,破線,実線が それぞれ Hurvitz タイプの条件である Δ1 > 0, Δ2 > 0, Δ3 > 0 の条件に 対応する境界線となっている.
提案安定判別法の有用性
提案した安定判別のアルゴリズムは, 一般化周波数変数φ(s) と 接続行列 A が与えられれば 系統的に安定性を判別できるアルゴリズム となっており,その有用性は以下の2点にある.
- システムの理解;個別サブシステムの動的性質を表す h(s) の特性と サブシステム間の相互作用を表す行列 A の特性の2つが陽に現れた表現と なっている.したがって,それ自身で大規模システムの理解につながる とともに.今後の一般化周波数変数を持つ線形システムの性能解析 において基本となる定理と考えられる.
- 計算量:システム G(φ(s)) の安定性は,Aφ に対するリアプノフ不等式 (LMI)を用いてもチェックできる.導出したLMIはそれに比べ,サイズの小さい ものとなっており,計算量の観点で優れている.
参考文献
1) S. Hara, T. Hayakawa, and H. Sugata : Stability analysis
of linear systems with generalized frequency variables
and its applications to formation control, In Proc. of the 46th
IEEE Conference on Decision and Control, 1459/1466 (2007)
2) 田中,原, 岩崎:“一般化周波数変数を持つ線形システムの安定性解析,”
第9回SICE制御部門大会 (2009)