研究背景
近年,非常に多くの要素どうしが相互作用を及ぼしあって振る舞いが規定される,大規模システムに関する研究が盛んに行われている.大規模システムに対しては,要素数が膨大であることに起因する問題から,従来の解析・制御手法を直接的に適用することが困難な場合が生じる.たとえば,生体内部の遺伝子調節機構では膨大な数のタンパク質が相互作用を及ぼしあうことでシステムを構築しているが,こういったシステムに対し,ひとつひとつの物質の状態に注目して解析・制御を行う従来の手法では,計算量や煩雑さの増加という観点から現実的とはいえない.
一方で,大規模システムの煩雑さを緩和する方法のひとつとして,数多くのモデル低次元化手法が提案されている.しかしながら,特に特異値分解を利用した平衡実現の打ち切りによる低次元化では,安定性は適切に保存されるも,一般にシステムの有する本質的な構造は保存されず,また平衡実現を得るためには多大な計算コストを要することが知られている.それとは別に,Krylov法が大規模システムに対して有効な低次元化手法として知られているが,一般に安定性の保存が保証されず,また低次元化によって生じる誤差の見積もりが事前に得られないことが知られている.
新たな視点にもとづく低次元化
例えば気体は,微視的には分子という個々の要素からから構成されているにも関わらず,その分子たる離散性を感じさせることはなく,巨視的には連続的な振る舞いをみせる.このことからも類推されるように,あるクラスの大規模システムは,ほとんど連続体としてみなして解析できると考えられる.
本研究では,拡散構造をもつ大規模システムに注目し,その拡散構造を保存した低次元化を行う.低次元化までの過程では,対象とするシステムが,適当なスケール変換を介した連続極限において,偏微分方程式で記述される拡散システムに漸近するという性質を利用する.
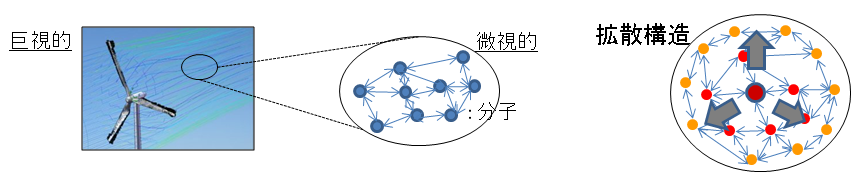
対象とするシステム
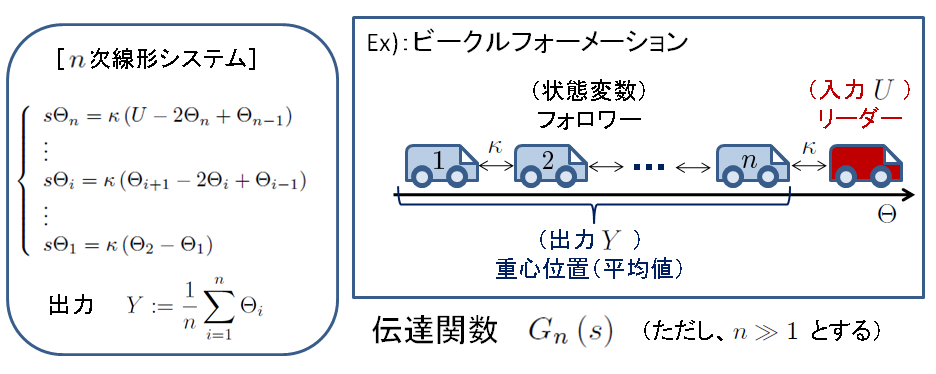
本研究では,以下の大規模線形システムを対象とする.このシステムの一例としてシンプルなビークルフォーメーションが考えられる.ここで入力Uはリーダーの位置,状態変数Θはフォロワーの位置,出力Yはフォロワーの重心位置(平均値)を表す.
低次元システムの導出過程
対象とするn次システムに対するm<n次の低次元システムの導出では, 対象とするシステムが周波数スケール変換を介した連続極限において拡散システムに漸近するという性質を利用する. 低次元システムはその拡散システムに対して異なる離散化を施すことによって導出される.
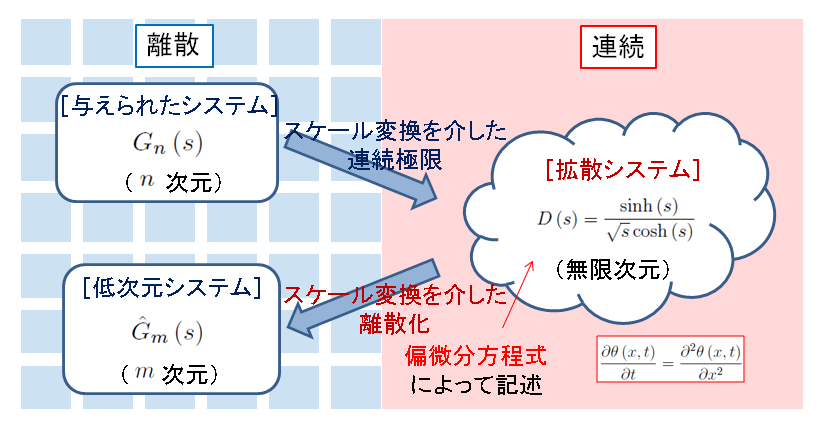
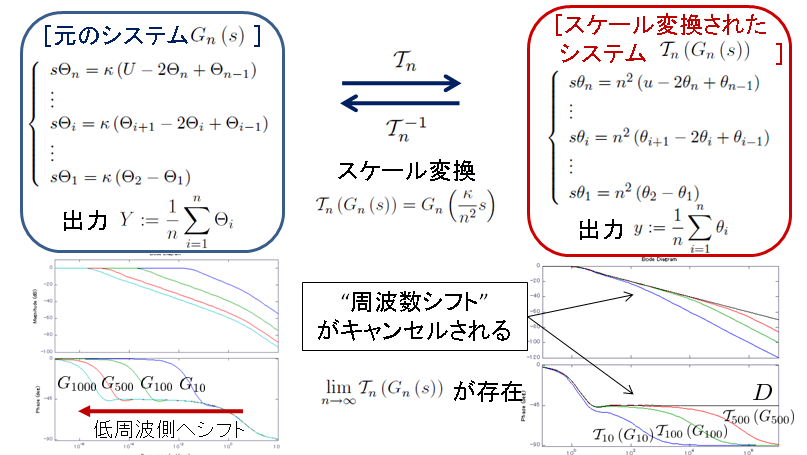
周波数スケールの変換
スケール変換前のシステムは,次数nの増加により,ボード線図(周波数領域における振る舞い)が低周波側に移動する.これは,システムが次数を増加させることで,より遅く振る舞うことを意味するが,ここで定義されるスケール変換によって,その移動が打ち消される.これにより,連続極限において拡散システムDに漸近する.
システム低次元化の過程
スケール変換が施されたシステムは,拡散システムDの一様な空間離散化モデルと解釈できる.したがって,Dに対して非一様な離散化を施すことによって異なる離散化モデルを導出する.これにより,低次元化問題は離散化メッシュの最適化問題に帰着される.
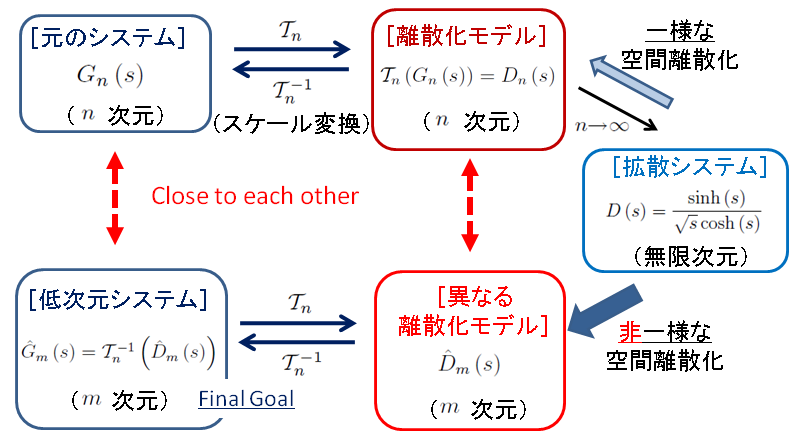
拡散システムの特徴を生かした離散化
連続極限において漸近する拡散システムは,入力が境界値に作用するため,拡散物質の空間的な変動は入力近傍が大きくなる.したがって,一様な離散化を施す場合と比べて,入力近傍を細かく離散化するほうが,拡散システムの特徴をより良く表現できる.つまり,少ない分割数(次数)により,同程度の特性を近似するモデルが導出できる.
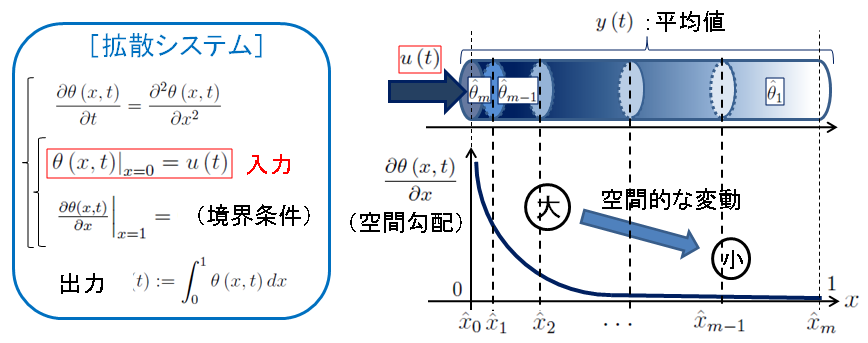
非一様空間離散化モデル
離散点の偏りをrでパラメトライズする(離散化された要素の長さは等比数列をなす) .このようにして得られた非一様な空間離散モデルは,rを変化させることによって,より少ない分割数により,一様な空間離散モデルと同程度の特性を表現することができる.
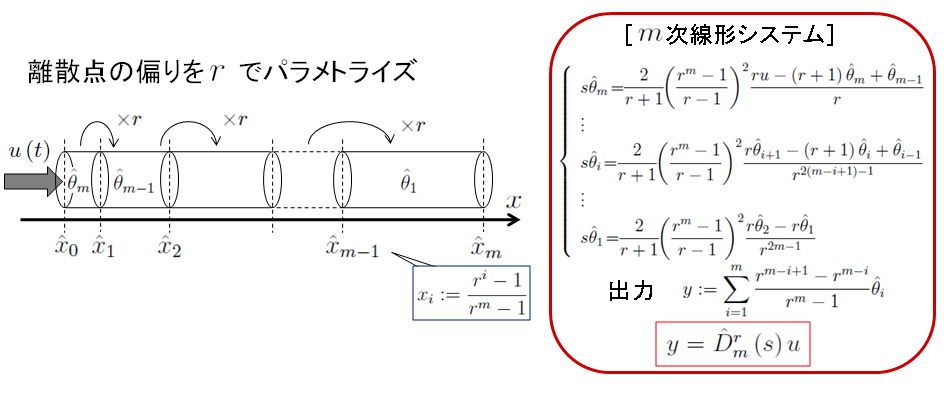
パラメータrの選定
離散化モデルどうしの大域的な特性解析は困難であるため,その低周波・高周波特性を良く近似する関数を新たに導出し, その関数に対して誤差評価を行う.これにより,評価は局所的となるが, 比較対象がともに拡散システムの離散化モデルであるため,十分な解析が可能である.
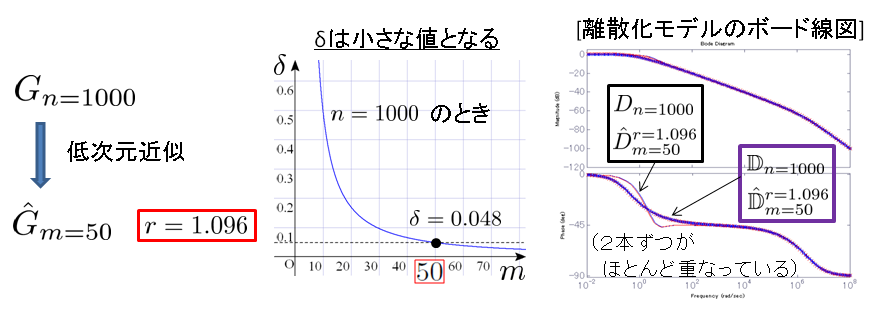
数値例
1000次のシステムを50次の低次元モデルで近似した結果が以下の通りである(※ボード線図においてスケール変換は平行移動に対応するため,離散化モデルのボード線図のみを示している).近似関数と離散化モデルの特性は中周波域で差が見られるが,本来評価したかった空間離散化モデルの特性は全帯域でほとんど一致している.

まとめ
本研究では,対象とするカスケードシステムが,スケール変換を介した連続極限において偏微分方程式で記述される拡散システムに漸近するという性質を利用することによって,システムの低次元化を行う新たな手法を提案した.こうして得られた低次元システムは,もとのシステムが有する拡散的な構造と安定性を保存し,かつ低次元化によって生じる入出力特性の誤差の評価が解析的に与えられる.ただし,それはシステムの近似関数に対する評価であるため,今後より慎重な議論を進める必要がある.
ここで扱ったシステムと同様に,適当な連続極限において,偏微分方程式で記述されるような連続体に漸近する大規模システムは,ほとんど連続体とみなして解析を行うことができると考えられる.本手法の他の大規模システムに対する適用可能性の検討は今後の課題となっている.
参考文献
1) 石崎,加嶋,井村:スケール変換を介した連続極限解析による大規模カスケードシステムの低次元化,第10回計測自動制御学会制御部門大会資料 (2010)
2) A.C.Antoulas: Approximation of Large-Scale Dynamical Systems, Society for Industrial Mathematics (2005)