研究の背景
近年,工学が扱うべき研究対象は,生体システム,通信ネットワーク,気象・環境を 始めとして急速に大規模・複雑化してきており,様々な分野で異なるアプローチに よる試みが盛んに行われてきている.制御の分野での大きな流れの一つは, マルチエージェントシステムの自律分散制御である.そこにおいて基本的な問い の一つは、「複数のエージェントが単独ではなしえないことが、互いに情報交換を行う ことによってなしえることは何か?」という協調によるメリットに関する問いである. 制御に限定すれば、最も基本的でありかつ満たさなければならない「安定性」に関する 性質で、以下の問いとなる.単独では安定化できないエージェントが.互いに何らかの 出力情報を共有し協力することにより,全体のシステムを安定にすることができるか?
研究の着眼点と目的
本研究では,マルチエージェントシステムに対する統一的な枠組みの一つとして 我々が提案している「一般化周波数変数を持つ線形システム」の枠組みで, 協調安定化問題を扱う.具体的には,最も基本的な問いの一つである 「ゲイン出力フィードバックによる安定化可能性」について議論する. すなわち,単独ではゲイン出力フィードバックによって安定化できないエージェントが、 互いに何らかの出力情報を共有し協力することにより定数ゲインフィードバックによって 安定化可能であるかどうかについて,理論的な解析を行う. この問題は,制御の観点から見て最も基本的な問いであるというだけでなく,振動子の ように不安定系をサブシステムとして持つ大規模系の安定化(同期)への応用が考えられる.
協調安定化可能性
厳密にプロパな有理関数 h(s) をダイナミクスとして持つ各エージェントが独自に ゲイン出力フィードバックによって安定化できるとき,”h(s) は単独安定化可能である” という.一方,n個のエージェントが互いに必要な情報交換をし,全体のシステムが安定に できるとき,”h(s) は協調安定化可能である”という.
上記の2つの安定化可能性の問題は,h(s) = n(s)/d(s) と置くと, 以下の2つの問題とそれぞれ等価である。
命題1:h(s) が単独安定化可能であるための必要十分条件は, d(s)+kn(s) が Hurwitz 安定となるような実数 k が存在することである. このとき,h(s) は”実ゲイン出力フィードバックで安定化可能 (Real-Gain Output Feedback Stabilizable: \Rstab)”という.
命題2:h(s) が協調安定化可能であるための必要十分条件は, d(s) + λn(s) が Hurwitz 安定となるような複素数 λ が存在することである. このとき,h(s) は”複素ゲイン出力フィードバックで安定化可能 (Complex-Gain Output Feedback Stabilizable: \Cstab)”という.
協調安定化可能性=単独安定化可能性
h(s) が単独安定化可能ならば協調安定化可能であることは自明である. また,次数の低い系など多くのクラスのシステムでは, それ自身で安定化できなければ複数のエージェントが協調しても安定化できない. 理論解析によって明らかにされたそのようなクラス, すなわち「協調安定化可能性=単独安定化可能性」が成立するクラスは, 以下の通りである.
- 2次系のすべて
- 3次以上の系で,分子多項式 n(s) が定数であるか,n(s)=ks, n(s)=k(s^2-b^2)
協調可安定であるが単独可安定でないシステムの例
4次のシステム h(s)=n(s)/d(s) で,単独では安定化できないが偶数個のエージェントが 協調することにより安定化できる例を示す.それは,以下で与えられる.
d(s) = (s-1)^2(s+1)(s+100),
n(s) = 100 (s+2) (19s^2/10 - s/500000 + 21/10)
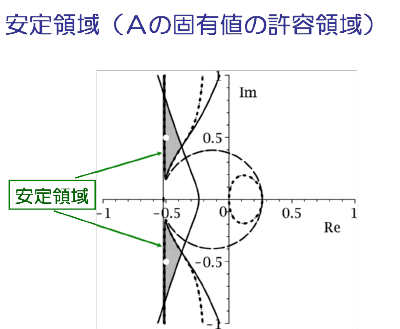
このシステムを安定化する出力フィードバックゲイン A の固有値が 満たすべき領域(安定領域)は,図のように与えられる. この安定領域が実軸を含んでいないことが,単独のゲイン出力フィードバックでは 安定化できないことを示している.
協調可安定出力フィードバック則
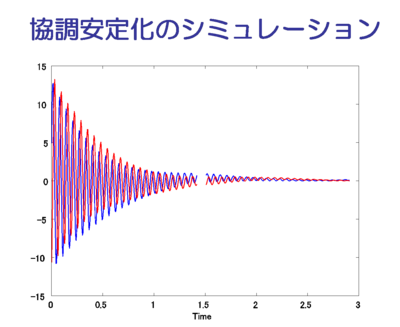
しかるに,2つのエージェントが協力し,以下のようなゲイン出力フィードバックを 行うと安定化できる(シミュレーションで確認).
u1 = - (y1 - y2)/2, u2 = - (y1 + y2) /2この制御則に対応する A 行列の固有値は (1±j)/2 で,安定領域に入っていることが 確認できる(安定領域の図の白抜きの○).
これは,制御工学的に素直に解釈できる. 2番目のエージェントは2つのエージェントの平均を小さくするように制御し, 1番目のエージェントは両者の差を小さくするように制御している. すなわち,2番目のエージェントがリーダの役割で全体の調和を図る動きをし, 1番目のエージェントはフォロアでリーダに追従する制御を行っている. このように各エージェントが同じ役割を果たすのではなく,違う役割を果たすことに よって初めて協調安定化が可能となる (2つのエージェントが同じ役割をする場合は A が対称行列となり,すべての固有値が 実数となるので、単独で安定化できないものはそのような制御則では安定化できない).
参考文献
1) 原, 管野, 田中:“ゲインフィードバックによる協調安定化可能性,” 第9回SICE制御部門大会 (2009)