研究の背景
制御対象の大規模化や複雑化に伴って,その解析や制御系設計には膨大な情報量と計算量が必要となるため,これまでのような直接的なアプローチには限界がある.このような状況を背景に,近年,互いに模倣し合うという概念である「双模倣性」を近似表現の設計原理に取り入れることで,システムの振る舞いをできる限り忠実に表現しつつシステム表現の簡単化を目指した,離散状態近似(discrete state abstraction)に関する研究が始まってきている.ただし,離散状態近似における離散状態の数が膨大になってしまうため,一般には小規模なシステムにしか適用できないのが現状であり,実用化を目指した,多分解能の視点からの展開が必要不可欠である.
研究の着眼点と目的
大規模複雑なシステムを表現するには,サブシステムの合成といった概念が重要である.しかしながら,従来の手法では離散状態化したサブシステム間の合成は双模倣性を満たさなかった.また連続状態の離散化も通常のグリッディングを基礎においているため, 離散状態の数の爆発を避けることはできないアプローチとなっている.
これに対して,本研究では,まず,離散状態近似が見通しよく展開できる「状態量子化埋込み表現」を提案し,離散状態近似の問題を状態量子化器の設計に帰着する.それをもとに,システムの近似誤差発展に応じて量子化メッシュを細分化することで多分解能化された離散状態近似表現を求める手法を開発する.つぎに,結合系における各サブシステムの近似双模倣性を新たに定義し,結合系の近似双模倣性を保証する条件を導出する.応用の一例として,障害回避問題(非凸拘束付最適制御問題)がある(文献4)参照).
離散状態近似
離散状態近似とは実空間上の非線形システムの解の振る舞いをオートマトン(ノードは有限状態,エッジは遷移関係を表す)として表現する.
近似双模倣性
近似双模倣性とは,おのおののシステムにおいて,もう一方のシステムの振る舞いを許容誤差内で追従する入力が存在する性質のことをいう
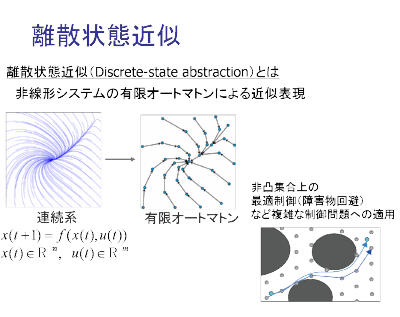

状態量子化埋込み表現の提案
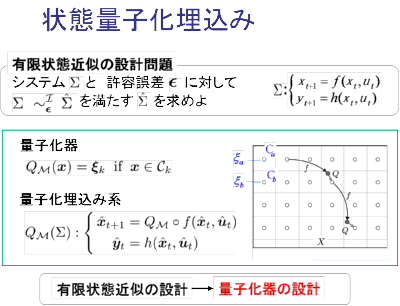
離散時間非線形システムに対して,量子化器を右図のように埋め込むと, 状態は自然に離散化され,オートマトン表現が得られる.これにより問題は, 量子化器の設計に帰着される.
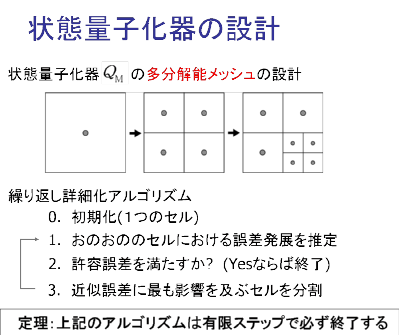
状態量子化器の設計
近似誤差を推定し,該当するセルを細分化することを繰り返すことで量子化器の多分解能メッシュを求める.近似誤差の推定に区間演算を用いる.
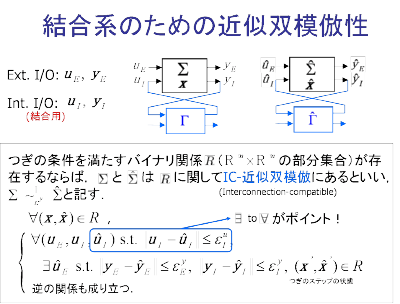
結合系の近似双模倣性と近似双模倣性条件
サブシステムの結合において近似双模倣性を保証するために, 外部入出力と内部入出力(結合用)の2種類の外部信号を導入した,より一般化された 近似双模倣性を定義する.そのもとで,2つのサブシステムの 近似双模倣系の結合系が,元の結合系と近似双模倣な関係を 保存するための条件を導出する.
この条件は,2つのサブシステムの近似双模倣系 間の結合点における最大近似誤差を許容するように保証するものである.

数値例による検討
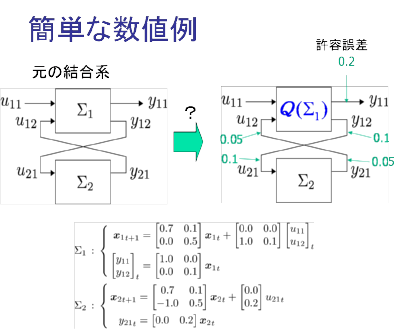
2つのサブシステムから成る結合系において, 出力近似誤差を0.2と指定して上位系のみ離散状態近似することを考える.
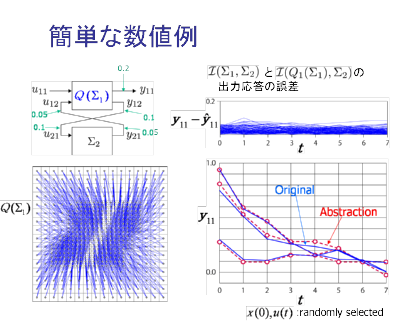
結果は下図のとおりである. この場合,得られた全体のモデルは, ある種の区分的アファインモデルとなっている.
さらなる展開
右図のように状態空間の一部に状態量子化器を埋め込むことにより,ある種の新しい形式の区分的アファインモデルが得られる.このように全系を近似するのではなく,非線形性の強いサブシステムなど部分的に離散近似する手法への拡張が考えられる.こうした問題を数値例では結合系の近似双模倣性を経由して解いたが,直接解くことが今後の展開として考えられる.

参考文献
1) Y. Tazaki and J. Imura, Bisimilar Finite Abstractions of Interconnected Systems, Hybrid Systems: Computation and Control (HSCC08), Lecture Notes in Computer Science 4981, Springer-Verlag, 514/527 (April, 2008)
2) Y. Tazaki and J. Imura, Finite Abstractions of Discrete-time Linear Systems and Its Application to Optimal Control, IFAC World Congress, 10201/10206 (July, 2008)
3) Y. Tazaki and J. Imura, Approximately Bisimilar Finite-state Modeling of Interconnected Systems, SICE annual conference, 3119/3124 (August, 2008)
4) 田崎,井村,状態量子化に基づく線形システムの離散状態近似とその最適制御への応用,計測自動制御学会論文集, Vol.44, No.10, 786/792 (2008)
5) Y. Tazaki, J. Imura, Discrete-state Abstractions of Nonlinear Systems using Multi-resolution Quantizer, to appear in HSCC09 (April, 2009).