研究の背景
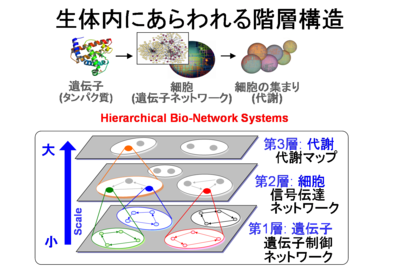
生体内では,多くの物質が複雑に相互作用し化学反応を起こすことで, 生命活動に必要な物質やエネルギーを生み出している.これらの反応は, 遺伝子・細胞などミクロなレベルから,各器官のマクロなレベルに至る まで,あらゆる箇所で生じており,それらの相互作用が調和して, 一つのシステムとして機能している.近年,このような複雑な生体化学 反応を数理モデル化し解析を行うことで,生命現象を予測し・解明しよう という研究が盛んである.
特に,体内時計など生体の基本的な機能と密接に関連していることが 明らかにされた”タンパク質の濃度の動的挙動”に関する研究は注目を 浴びている.その理由は,タンパク質合成に関与する遺伝子制御ネット ワークの性質を調べることで,生物学的・医学的に重要な知見を得られる 可能性がある点にある.一方,構成的生物学(Synthetic biology)の分野 では,このような生体内の反応に着目し,人工的に作成した遺伝子回路を 用いて,振動子やスイッチなどの従来の電気的な素子に代わる生体素子を 作成する実験も盛んに行われている.これらの素子の作成においても, 所望の回路を実現するために遺伝子回路が満たすべきパラメタなどを 解析することが重要である.
研究の着眼点と目的
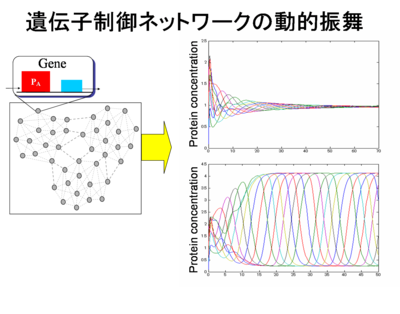
実際に観察される生体の遺伝子制御ネットワークでは,タンパク質濃度の 振舞は大きく分けて以下の2種類存在する.
- 濃度が平衡点に収束(外的環境の変化に対する恒常性)
- 濃度が周期振動(体内時計など生体に必要な機能を得るために必要)
本研究では,非線形システムとしてモデル化される遺伝子制御ネットワーク のダイナミクスを用い,これらの動的振舞を解析する.これまでの動的挙動の 解析は,遺伝子数と反応経路を定めた上での個別な解析となることが多く, 一般的に議論をするのは難しかった.これに対し本研究では,制御理論を ベースに系統的かつ理論的な解析を行う.
具体的には,反応経路を「環状に連なる反応」と限定することで,遺伝子数に 依存しない動的挙動の解析手法を示す.本研究のアプローチのキーポイントは, 遺伝子が増えることにより大規模になるシステムを一般化周波数変数を持つシス テムと捉えなおし、系統的に解析を行うことである.
環状遺伝子制御ネットワーク
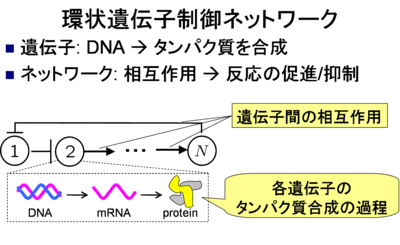
本研究では,下図のように反応が環状に連なる遺伝子制御ネットワーク におけるタンパク質濃度の動的挙動を パラメタに関して解析する. 環状遺伝子制御ネットワークは,生体内に存在する 基本的で重要な遺伝子制御ネットワークの1つであり, 人工的に設計した遺伝子振動子である Repressilator[Elowitz & Leibler, 2000] の機構としても用いられている.
遺伝子制御ネットワークのダイナミクス
N個の遺伝子で構成される遺伝子制御ネットワークのダイナミクスは 2N個の非線形微分方程式を用いて次のようにあらわされることが 知られている. 本研究では, この非線形システムの動的挙動をパラメタk_m, k_p, α,βに 関して解析する.

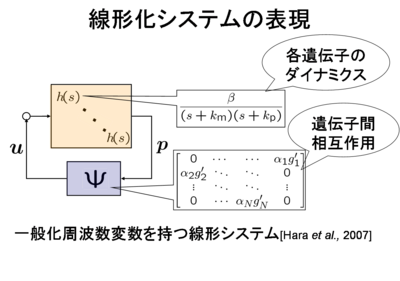
線形化システムの表現
遺伝子数Nの遺伝子制御ネットワークの平衡点の局所安定性は, 平衡点におけるサイズ2N×2Nのヤコビ行列の安定性に帰着されるが, Nが大きくなるとその解析が困難になる.これを解決するため, 線形化システムを下図のように書き直し,一般化周波数変数を持つ 線形システム[Hara et al., 2007] と捉え,任意のNに対して統一的 に適用できる図的および解析的な安定条件を求める.遺伝子制御ネットワークの図的な安定条件
図的な安定条件は,2次のシステムである各遺伝子のタンパク質 合成ダイナミクスから定まる複素平面状の領域と,遺伝子間相互 作用を表す行列ψの固有値の関係として表現できる(定理1), 行列ψの固有値がある円周上に乗っている性質を用いることで, 簡単に安定判別ができる.
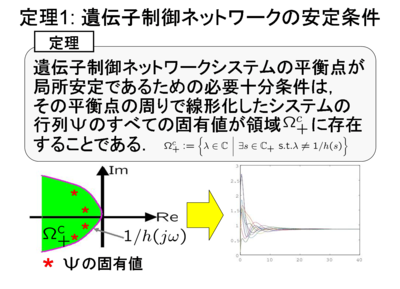
数値例: 図的な安定条件
図的な安定条件の実行は、以下の3つのステップからなる (具体的には,数値例を参照).
- 平衡点を求め,線形化モデルを求める
- 各遺伝子のダイナミクスから定まる緑色の安定領域を 描く
- 遺伝子間の相互作用を表す行列ψの固有値を描く
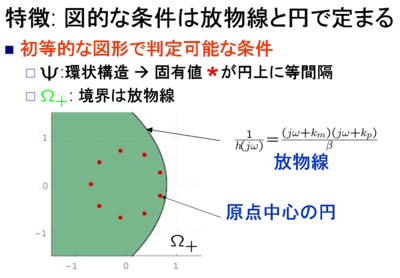
図的な条件の特徴
定理1の特徴は,これらの領域と固有値が,「放物線」と「円上」 という初等的な図形で描ける点である.この特徴は,遺伝子数Nに 依らず常に成立するため,遺伝子数が多くなっても容易に解析が 可能である.
タンパク質濃度の周期振動現象
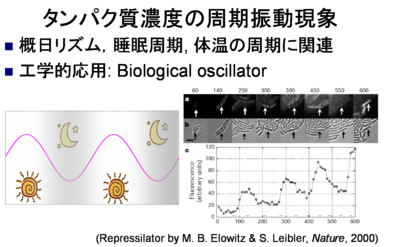
タンパク質濃度の「周期振動現象」も以下の2つの理由により重要であり, その理論的解析を行う.
- 生命現象の解明:タンパク質濃度の周期振動が及ぼす生体の 周期現象(概日周期や睡眠周期など)の理論的解析
- 工学への応用:周期振動現象の工学的応用の可能性の追求.例として, 人工的な遺伝子回路を用いて製作された振動子Repressilator[Elowitz & Leibler, 2000].
システムのωリミットセット
Poincare-Bendixson型の定理[J.M. Paret et al., 1990]を適用すること により,システムのωリミットセットは平衡点もしくは周期振動のいずれか であるとなることを示すことができる.また,システムの平衡点が唯一で あることも示すことができる.したがって,唯一の平衡点のまわりで線形化した システムの「不安定性」が周期振動の存在条件を解析する上で重要となる.
周期振動の存在条件(図的な条件)
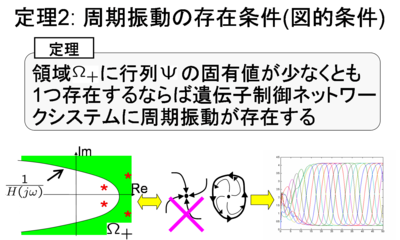
以上の議論を総合すると,周期振動の存在を図的に確認できる定理が 導かれる.この条件は,遺伝子数Nによらず,円上の固有値と放物線で 区切られる領域の関係で定まるため,遺伝子数が増えても確認しやすい という特徴がある.
周期振動の存在条件(解析的な条件)
図的な条件の特徴を生かして,初等的な図形を数式で書き下し, 解析的な周期振動条件を求めることができる. 不等式の左辺は,遺伝子間の相互作用を表すパラメタで計算でき, 右辺は,各遺伝子のダイナミクスから計算できる.

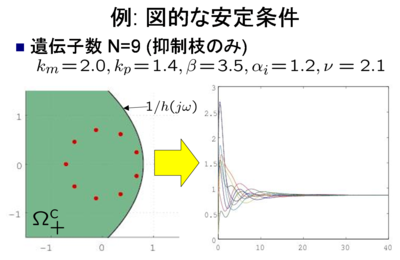
数値例: 図的な周期振動の存在条件
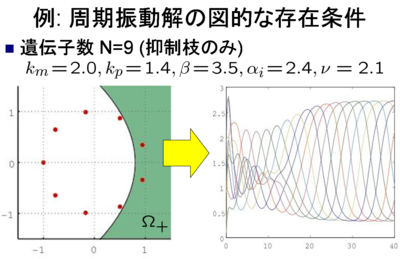
抑制枝だけからなる遺伝子数N=9の遺伝子制御ネットワークを考える. 行列Ψの固有値のうち2つが不安定領域Ω_+に存在するので,定理2より, この遺伝子制御ネットワークに周期振動が存在することがわかる. 実際,シミュレーションにより周期振動が生じることが確認できた.
参考文献
1) T.-H. Kim, S. Hara, T. Fujikawa and J. Harada, ``Stability analysis of gene-protein regulatory networks with cyclic activation-
inhibition connections,'' 第51回自動制御連合講演会予稿集, pp. 1154--1159, 2008.
2) 堀, 原, 金, 環状遺伝子制御ネットワークにおける周期振動の存在条件, 第9回SICE制御部門大会予稿集, 2009.