研究の背景
ネットワーク技術の進歩により、工学が扱う対象は大規模・複雑化してきており、 このようなシステムを解析・設計する統一的な手法の確立が望まれている。 また、生物・生体系や気象など大規模系はそのまま扱うのは難しく、それらの分野 においては大規模な系を適切に階層化表現し解析する手法の確立が必要不可欠である。 このようなシステムは一般に、空間・時間・周波数など様々な側面において異なる スケールを持つ複数のサブシステムが相互に作用しあう異種相互作用系であると 捉えることができ、一つの方向として多分解能動的システム(異なる分解能・スケール を持つ動的システム)に対するシステム論の確立の重要性が指摘されている。
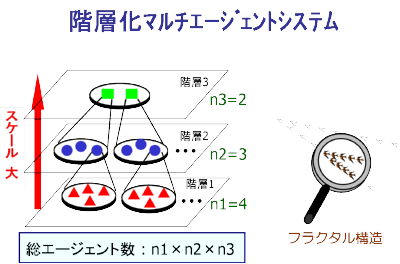
研究の着眼点と目的
多分解能動的システム論を展開するに当たりキーとなるのは、その枠組みを与える モデルの表現形式である。 そこで本研究では、階層化マルチエージェントシステム(右図参照)を対象として、 自己相似性を持つ階層化システムの比較的一般的な表現形式を与え、 その階層間を接続する行列の性質に着目した安定度解析を行う。 階層間の接続を表す行列の性質としては、これまで小ゲイン性(連結強度が小さい) やスパース性(連結リンク数が小さい)が主に取り扱われてきた。
これに対し本研究では、これまで検討されてこなかった「接続行列の低ランク性」に 焦点を当てる。その理由は以下の通りである。階層化されたシステムにおいて、 階層間の情報伝達は接続行列を通してなされるが、そこでは情報が圧縮されて伝達 されると考えることができ、この圧縮がランク落ちに対応すると捉えることが できるからである。 実際、巡回型の情報取得が可能な自己相似構造を持つシステムに対して、 階層化の情報構造を有する接続行列の固有値解析をに基づいた安定度の解析を行い、 低ランク性を持つ階層間接続の優位性を示すとともに、シミュレーション結果により 確認を行っている。
階層化マルチエージェントシステムの表現
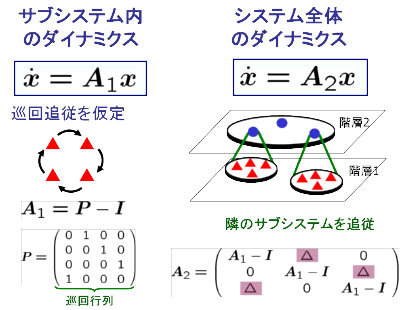
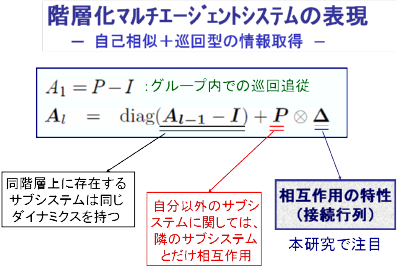
自己相似性(フラクタル構造)を有する階層化マルチエージェントシステムは、 サブシステム内の情報構造に基づくサブシステムのダイナミクスを表す微分方程式 (通常のマルチエージェントシステムの表現)を階層間の情報構造に基づいて 逐次的に定義することができる。
巡回追従のケースで階層が2の場合の例を示したのが右の図で、一般には A 行列も 逐次的に定義できる。このとき、相互作用の特性を表す接続行列⊿が重要な 役割を果たす。
接続行列の特性と提案モデルの直感的理解
階層間の接続行列は、何らかの意味で弱いものでなければならない。 従来は、疎性あるいは小ゲイン性で結合の弱さを表現している場合がほとんどで あった。ここでは、接続行列の低ランク特性に着目する。
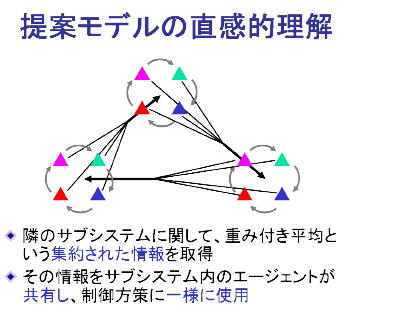
- 隣のサブシステムに関して、重み付き平均という集約された情報を取得
- その情報をサブシステム内のエージェントが共有し、制御方策に一様に使用 これらの意味づけは、収束の速い合意形成に大きな働きをする。

固有値分布
「接続行列=単位行列」の場合の行列 A の固有値分布は、Smith らによって 求められている。
「接続行列=ランク1行列」の場合も、行列 A が階層化 された巡回行列であるという性質を使うと、定理のように求めることができる。


安定度解析
上記の固有値分布に関する定理を用いると、安定度解析(収束率および減衰率) を行うことができる。その結果が、命題1(収束率:虚軸に最も近い非零の固有値 によって決定)と命題2(減衰率:虚軸から角度の意味で最も近い非零の固有値 によって決定)である。
収束率・減衰率ともに、ランク1行列の方が単位行列の 場合に比べ優れている(少なくとも悪くはならない)ことが理論的に明らかに されている。


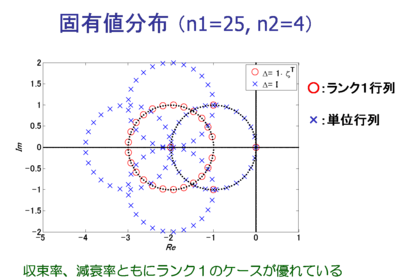
数値例題(n1=25, n2=4)による確認
上記の固有値分布を n1=25, n2=4 の場合にプロットし、収束率および減衰率を 比較した。 どちらともランク1行列の方が優れていることが確認できる。
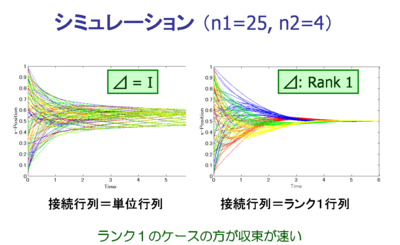
また、シミュレーション実験を行い、ランク1行列の方が収束速度が速いという 意味で優れていることが確認できる。
拡張
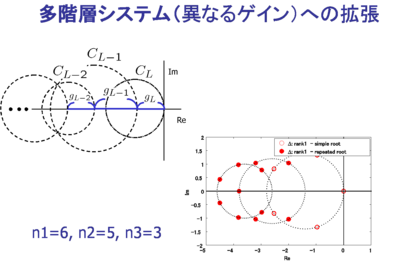
上記の固有値分布に関する定理は、多階層システムで階層間で異なるゲインを 有する場合にも容易に拡張できる。
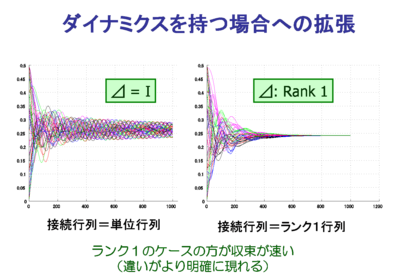
また、各エージェントがダイナミクスを持つ場合にも、一般化周波数変数を持つ システムに対する安定条件を適用することにより拡張可能で、 ランク1行列の優位性がより明確に現れる。
参考文献
1) 清水, 原:“階層化マルチエージェントシステムにおける階層間接続行列の
性と安定度,” 第8回SICE制御部門大会 (2008)
2) H. Shimizu, S. Hara:“Cyclic Pursuit Behavior for Hierarchical Multi-agent
Systems with Low-rank Interconnection,”
SICE Annual Conference 2008, Chofu, Tokyo, Japan (August, 2008)