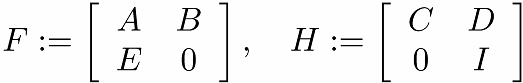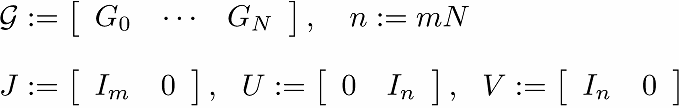一般化KYP補題とは?
?
KYP補題(Kalman-Yakubovich-Popov)は、与えられたシステムの周波数特性の条件を線形行列不等式(LMI)で表される等価な条件に変換するものである。正実性補題や有界実補題(小ゲイン条件)が典型的な例としてしられており、LMIに基づくH∞制御系設計の基礎となっている。しかし、これまでのKYP補題は、すべての周波数帯域に亘る特性だけを対象としていたため、低周波域・高周波域といった注目すべき特定の周波数に限定した特性を取り扱うためには周波数に依存した重み関数の導入が必要であった。したがって、複数の周波数帯域毎のきめ細かな周波数整形を行うにはKYP補題を有限周波数帯域を対象としたものに一般化する必要がある。
一般化KYP補題(GKYP Lemma) は、この目的を達成するためにKYP補題を以下の点で一般化しかつ統一的な表現にしたものである。
?(1) 取り扱える周波数変数の統一的表現を導入し、連続時間系・離散時間系の低周波帯域・中間周波数帯域・高周波数帯域に対する周波数特性条件を統一的に表すLMI条件を求めた。
?(2) 対象となるシステムの一般化を図り、デスクリプタシステムや多項式システムも統一的に扱える。
?(3) 取り扱える周波数特性の拡張を図り、複素平面の任意の2次関数の内部・外部が統一的に取り扱える。
通常のKYP補題は、以下で与えられる。
Standard KYP Lemma
通常のKYP補題は、以下で与えられる。
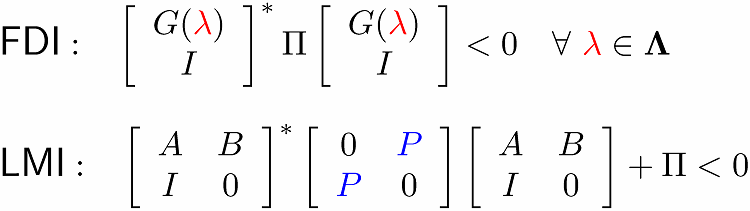
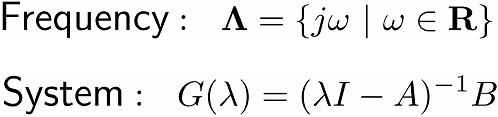
周波数変数の一般化と対象システムの拡張
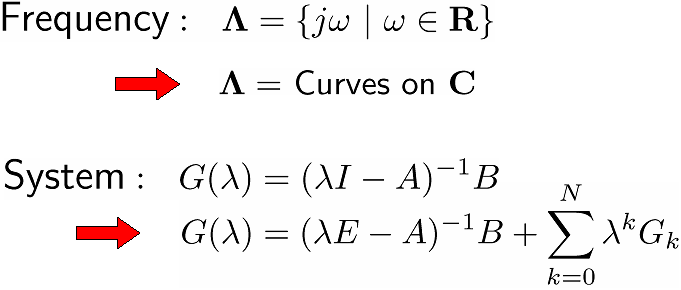
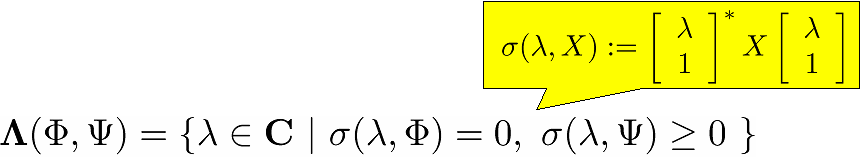
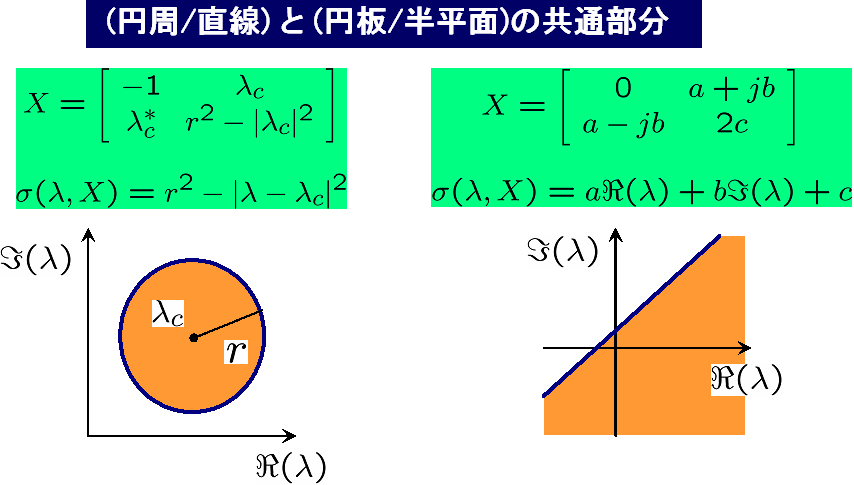
?
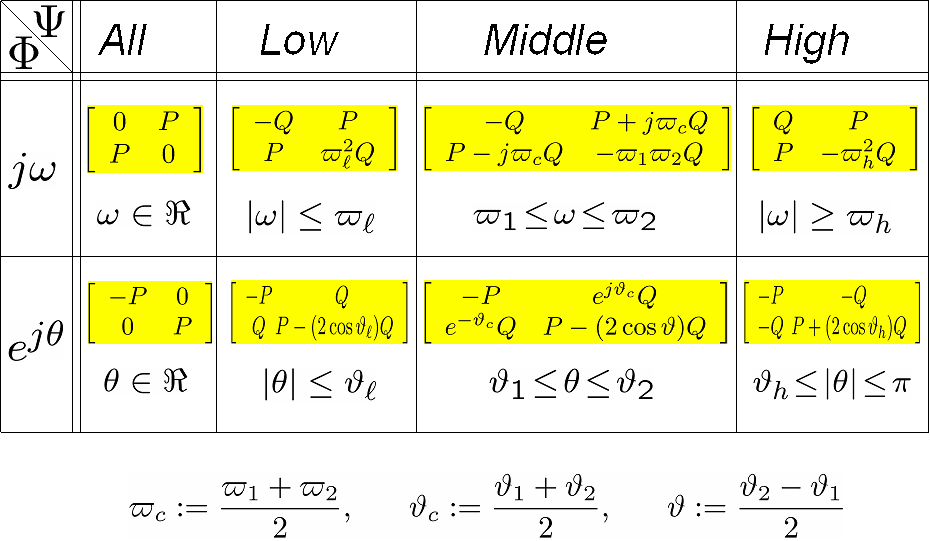
例えば、連続時間系・離散時間系の場合は、以下のようになる。
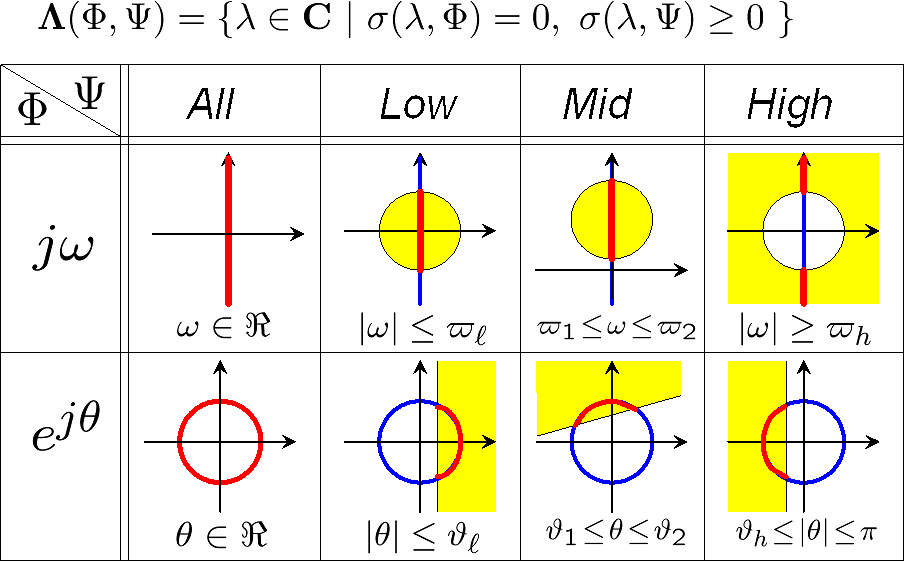
連続時間系・離散時間系の場合
例えば、連続時間系・離散時間系の場合は、以下のようになる。

一般化KYP補題
?一般化KYP補題(GKYP Lemma) は、以下で与えられる。


?ここで、連続時間系・離散時間系の場合の は
は

?
デスクリプタシステム・多項式システムに対する結果
デスクリプタシステムや多項式システムに対する具体的な結果は以下の通りである。