ハイブリッド凸関数

　　関数 が凸拡張可能であるとき、 をハイブリッド凸関数と言う。ここで、関数 が凸拡張可能であるとは、ある凸関数  が存在して、

が成り立つことである。

　ハイブリッド凸関数の中でよい構造をもったクラスを明らかにするため、離散凸解析 （Discrete Convex Analysis）の枠組みに基づき、ハイブリッドL凸関数を定義する。

ハイブリッドL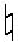凸関数

　　関数 が次の条件を満たすとき、ハイブリッドL凸関数と言う。

　あるL凸関数  、ある正則行列  、ベクトル  が存在して、

が成り立つ。

ここで、L凸関数は離散凸解析 （Discrete Convex Analysis）により、次のように定義される。

　閉真凸関数  が次の並進劣モジュラ性を満たしているとき、L凸関数であるという。

（並進劣モジュラ性）

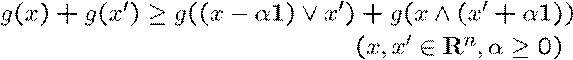
ここで、

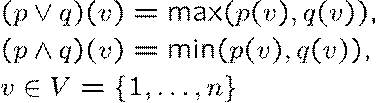
とおいている。

　ハイブリッドL凸関数に対して、高松・原・室田により、最適性規準が導出されている。

ハイブリッドL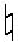２次凸関数

　　特に関数 が２次関数のとき、ハイブリッドL凸関数は次のようになる。

[命題１: ハイブリッドL凸2次関数 (高松-原-室田) ]
2次関数

がハイブリッドL凸関数であるための必要十分条件は，行列 が正定かつある正則行列 に対し，行列

が次の2条件を満たすことである。

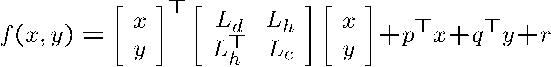
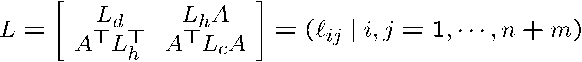
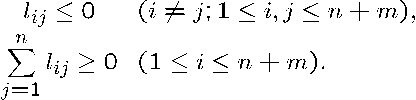
[例: ハイブリッドL凸2次関数]
２変数の2次関数

は、たとえば とすると、行列 が命題1における２条件を満たすので、ハイブリッドL凸関数である。
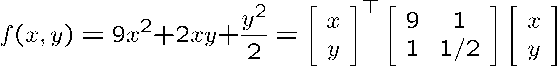
下図に を示す。

トップページへ