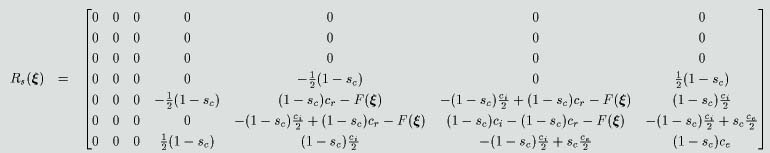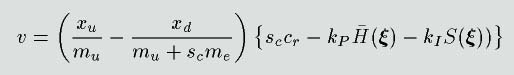エネルギー保存制御
本研究の目的は定常跳躍という周期運動の実現です。
一般に、周期的な挙動を示すシステムには何らかの保存量が存在します。特に、周期的な
運動を行うメカニカルシステムにおいては力学的エネルギーがその保存量にあたります。
実際に、歩行や跳躍などの運動における力学的エネルギーの総和は一定もしくは概周期的な
値をとります。
そこで、逆に物理システムにおいてエネルギーを一定に保持した場合を考えてみましょう。
この場合、システムの挙動は特定の状態にとどまるか、周期的なものになると予想されます。
この考えに基づき、定常跳躍を実現するために、ハミルトニアンの目標値
 を設定し、実際のハミルトニアン
を設定し、実際のハミルトニアン
.jpg) を
を
 に収束させる状態フィードバックコントローラを導出します。コントローラは
Interconnection and Damping Assignment - Passivity Based Controlに基づく
Damping-Injectionの原理を利用して設計します。
に収束させる状態フィードバックコントローラを導出します。コントローラは
Interconnection and Damping Assignment - Passivity Based Controlに基づく
Damping-Injectionの原理を利用して設計します。
Damping-Injectionの原理
まず、Damping-Injectionの原理について簡単に説明します。
PCHシステムに状態フィードバック
を施したときの閉ループ系が
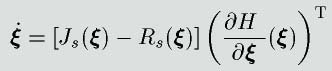
で表されるとき、ハミルトニアンの時間微分は
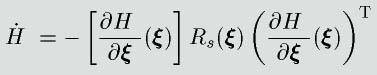
と表すことができます。この式より、ハミルトニアン
.jpg) の挙動は
の挙動は
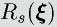 をフィードバックによってどのように選ぶかによって決まることがわかります。
そこで、望ましい閉ループ系の消散行列をもたらすフィードバック制御則を導出します。
をフィードバックによってどのように選ぶかによって決まることがわかります。
そこで、望ましい閉ループ系の消散行列をもたらすフィードバック制御則を導出します。
コントローラの導出
コントローラにより、閉ループ系の消散行列
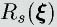 をハミルトニアンと目標値の偏差に比例した状態フィードバックの形になるようにおくことで、
ハミルトニアンを目標値へ収束させます。望ましい閉ループ系の消散行列の形は、
をハミルトニアンと目標値の偏差に比例した状態フィードバックの形になるようにおくことで、
ハミルトニアンを目標値へ収束させます。望ましい閉ループ系の消散行列の形は、
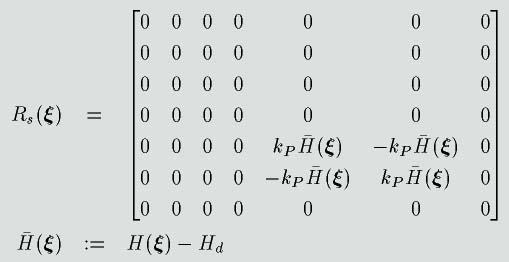
なのですが、実際には
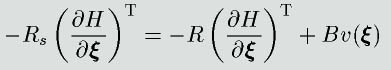 (★)
(★)
を満たさなければならず、また付加した仮想コンプライアンスを打ち消さないようにするために、
この形にすることはできません。これらを考慮した結果、
閉ループ系の消散行列
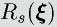 の形は
の形は
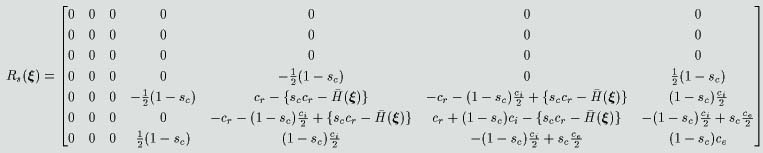
となります。
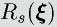 の中に打ち消せずに残ってしまう項と、着陸時の衝突衝撃のために、
ハミルトニアンを常に目標値に収束させておくことは不可能です。
よって離陸時に切断面を設け、その切断面でのみ更新される離散的な積分項を導入
することにより、離陸時においてはハミルトニアンが目標値に収束するようにします。
各切断面通過時刻を
の中に打ち消せずに残ってしまう項と、着陸時の衝突衝撃のために、
ハミルトニアンを常に目標値に収束させておくことは不可能です。
よって離陸時に切断面を設け、その切断面でのみ更新される離散的な積分項を導入
することにより、離陸時においてはハミルトニアンが目標値に収束するようにします。
各切断面通過時刻を
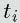 とすると
導入される離散的な積分項
とすると
導入される離散的な積分項
.jpg) は
は
eq.jpg)
となります。最終的な閉ループ系の消散行列
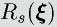 は
は
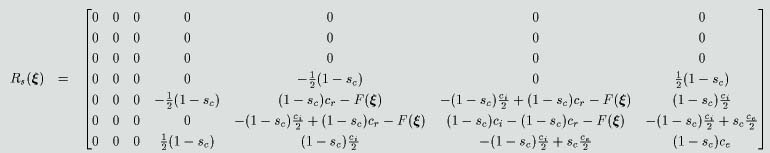
ただし
.jpg)
となります。このとき式(★)より、導出されるコントローラは
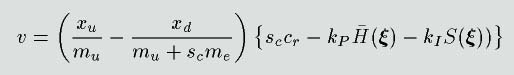
となります。
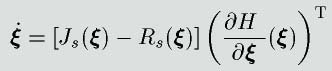
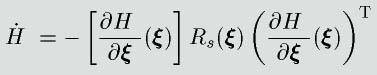
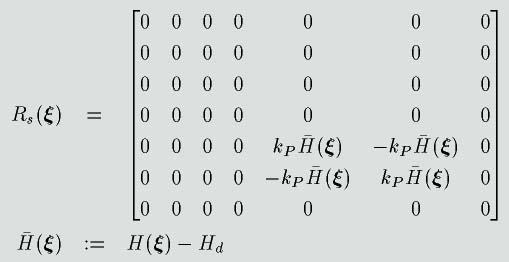
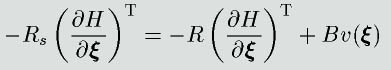 (★)
(★)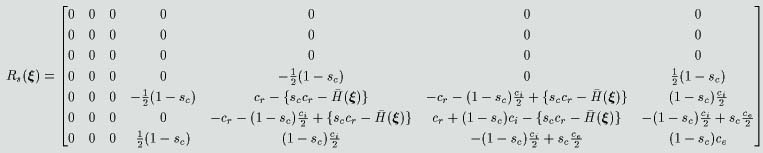
eq.jpg)