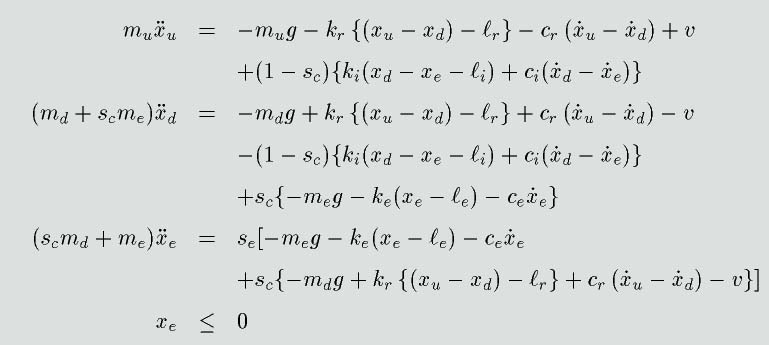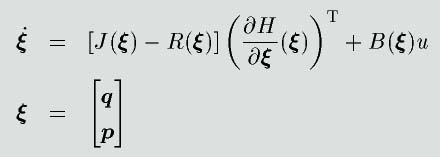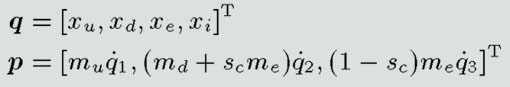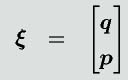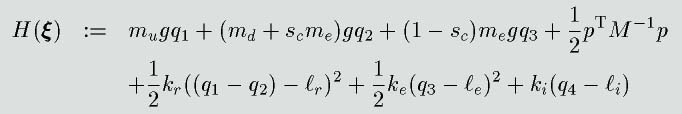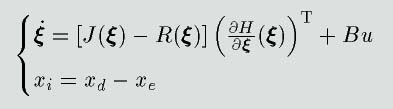モデリング
仮想コンプライアンスを付加した跳躍ロボットの運動方程式は
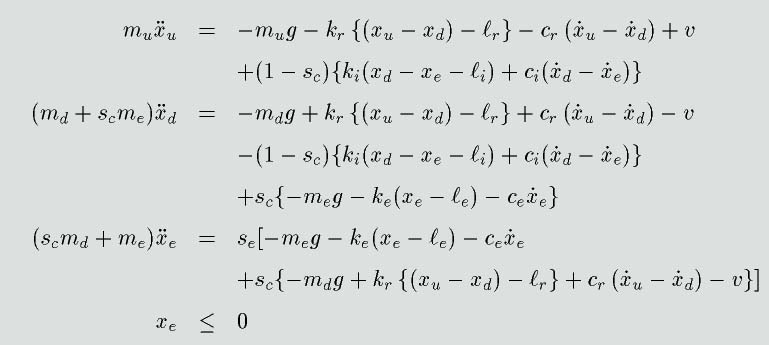
となります。ここで、
 は飛遊相・接地相で切り替わる2値変数、
は飛遊相・接地相で切り替わる2値変数、
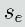 は環境の位置によって切り替わる2値変数です。
この運動方程式を、システムのエネルギーを陽に表現した構造を持つ
Port-controlled Hamiltonianシステム表現で表すことにします。
は環境の位置によって切り替わる2値変数です。
この運動方程式を、システムのエネルギーを陽に表現した構造を持つ
Port-controlled Hamiltonianシステム表現で表すことにします。
Port-controlled Hamiltonianシステム表現とは
Port-controlled Hamiltonian(以後PCH)システム表現とは、
ハミルトニアンシステムを以下の3点
- 構造行列Jは歪対称行列に拡張
- 消散行列Rの導入
- 制御入力uの追加
について拡張したものであり、次式のような状態方程式
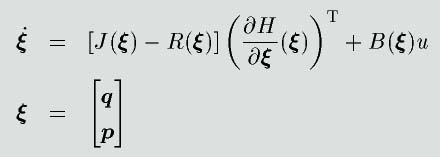
で表されます。ここで、状態量
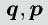 はそれぞれ位置を表す一般化座標ベクトル、および運動量を表す一般化運動量ベクトル
と呼ばれ、スカラ関数
はそれぞれ位置を表す一般化座標ベクトル、および運動量を表す一般化運動量ベクトル
と呼ばれ、スカラ関数
.jpg) はハミルトニアンと呼ばれる関数で、システムの力学的エネルギーの総和を表します。
はハミルトニアンと呼ばれる関数で、システムの力学的エネルギーの総和を表します。
システムのPCH表現
上で示したシステムの運動方程式をPCHで表現することを考えます。研究を進めた結果、
そのままPCH表現を行うと、構造行列Jおよび消散行列Rが複雑になり、
後におこなうコントローラの導出が困難になることが分かりました。
そこでまず、形式的に冗長な状態変数
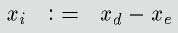
を導入します。つぎにこの
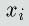 を加えた一般化座標
を加えた一般化座標
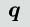 および一般化運動量
および一般化運動量
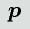 を
を
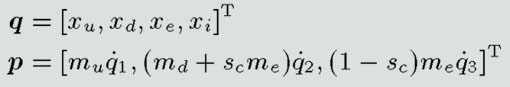
とし、この
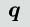 および
および
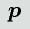 をまとめて状態ベクトル
をまとめて状態ベクトル
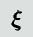 を
を
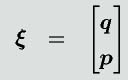
とします。さらに、ハミルトニアン
.jpg) をシステム全体の力学的エネルギーの関数として
をシステム全体の力学的エネルギーの関数として
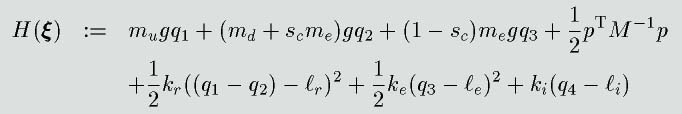
と定義します。このハミルトニアンを用いることにより、システムの運動方程式は
以下のようなPCHシステム表現
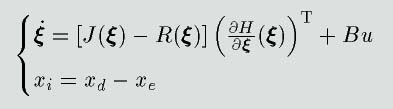
ただし


に表すことができます。