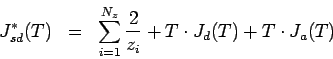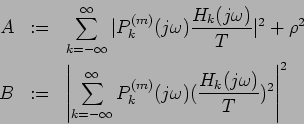次へ: 文献目録
上へ: 達成可能な制御性能限界 - 制御しやすい制御対象の設計を目指して -
戻る: 連続時間制御の場合
図に示すサンプル値制御系を考える。
ここで、制御対象 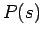 は連続時間系であるが、制御器
は連続時間系であるが、制御器 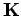 は
離散時間系
は
離散時間系 ![$K_d[z]$](img11.png) とアンチエリアシングフィルタ
とアンチエリアシングフィルタ 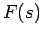 、
理想サンプラ
、
理想サンプラ 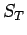 、零次ホールド
、零次ホールド 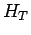 で
構成されており、サンプリング周期は
で
構成されており、サンプリング周期は 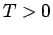 とする。
なお、零次ホールド
とする。
なお、零次ホールド 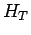 の伝達関数
の伝達関数 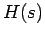 は
は
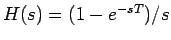 で与えられることに注意しておく。
で与えられることに注意しておく。
図 2:
サンプル値制御系
 |
いま、ナイキスト周波数を
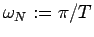 と定義し、伝達関数
と定義し、伝達関数 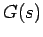 の高調波成分を表す伝達関数
の高調波成分を表す伝達関数 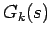 を
を
と表し、
![${\cal Z}[\cdot]$](img23.png) を零次ホールド等価な伝達関数を表すとする。
このとき、達成可能な
を零次ホールド等価な伝達関数を表すとする。
このとき、達成可能な 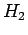 制御性能
制御性能 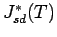 は、以下の定理で与えられる。
は、以下の定理で与えられる。
[定理2]
ただし、
ここで、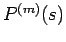 は
は 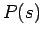 の最小位相部分を表す伝達関数で、
の最小位相部分を表す伝達関数で、
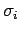
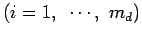 は、
は、
の単位円外の零点である。
上記の結果から、以下のことわかる。
- 上記の結果において、第1項は取り除くことができない
連続時間系の不安定零点の影響である。
- 第2項と第3項はいづれも非負で、
それぞれ離散化零点の影響とエイリアシングの影響を表している。
- 例え制御入力に対するペナルティーを無くしても、すなわち
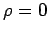 としても第2項と第3項は零とはならない。これが、サンプル値制御を
行うときに付加された性能限界の量で、サンプリング周期
としても第2項と第3項は零とはならない。これが、サンプル値制御を
行うときに付加された性能限界の量で、サンプリング周期 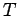 を
零に近付けていくと、1次のオーダで零に近付いていくことが
確認できる。
を
零に近付けていくと、1次のオーダで零に近付いていくことが
確認できる。
Okajima Takashi
平成16年7月7日
![]() は連続時間系であるが、制御器
は連続時間系であるが、制御器 ![]() は
離散時間系
は
離散時間系 ![]() とアンチエリアシングフィルタ
とアンチエリアシングフィルタ ![]() 、
理想サンプラ
、
理想サンプラ ![]() 、零次ホールド
、零次ホールド ![]() で
構成されており、サンプリング周期は
で
構成されており、サンプリング周期は ![]() とする。
なお、零次ホールド
とする。
なお、零次ホールド ![]() の伝達関数
の伝達関数 ![]() は
は
![]() で与えられることに注意しておく。
で与えられることに注意しておく。
![]() と定義し、伝達関数
と定義し、伝達関数 ![]() の高調波成分を表す伝達関数
の高調波成分を表す伝達関数 ![]() を
を