有限周波数条件に基づく''制御しやすいシステムの特徴付け''
制御しやすい機構の性質として機構設計の立場では、 "振動モードの同相性"
(その振動モードの運動方向が剛体モードの運動方向と 一致していること)が知られている。
しかし、この概念はモード分解に基づくものであるので、 システム論的な展開には向いていない。
そこで、この概念をシステム制御論的に発展させたものとして、 「有限周波数正実性」という性質を導入した。
具体的には、「動的な位置フィードバック制御器で達成できる 制御帯域 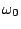 は概略以下に示す周波数と一致する。」という
事実に基づくものである。
は概略以下に示す周波数と一致する。」という
事実に基づくものである。
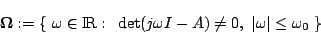
の条件を満たすとき、帯域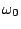 で
有限周波数正実(Finite Frequency Positive-Real:FFPR(
で
有限周波数正実(Finite Frequency Positive-Real:FFPR(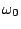 ))
であるという。
))
であるという。
を満たす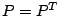 ,
, 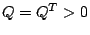 が存在することである。
が存在することである。
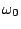 以下の周波数をもつすべてのモードが同相。
以下の周波数をもつすべてのモードが同相。
- 制御対象
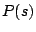 が与えられているとき,
が与えられているとき,
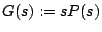 が
が
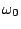 以下のすべての周波数で正実。
以下のすべての周波数で正実。
[定義1]
正方の伝達関数![]() は、
は、
の条件を満たすとき、帯域
したがって,制御しやすい制御対象は、この有限周波数正実性によって
特徴づけられることになる。
そこで、より高い周波数 ![]() に対して FFPR となるように,
制御対象を設計するのが目標となる。
それに有効なのが、以下に示す有限周波数正実となるための
線形行列不等式(LMI)形式の必要十分条件である。
に対して FFPR となるように,
制御対象を設計するのが目標となる。
それに有効なのが、以下に示す有限周波数正実となるための
線形行列不等式(LMI)形式の必要十分条件である。
[定理3]
正方の伝達関数行列
![]() ,
および正の実数スカラ
,
および正の実数スカラ![]() が与えられているとする。
このとき,
が与えられているとする。
このとき,![]() が
FFPR(
が
FFPR(![]() ) となるための
必要十分条件は、
) となるための
必要十分条件は、
を満たす
上記の条件は明らかに変数 ![]() と
と ![]() に関する線形行列不等式条件であり、
与えられた伝達関数
に関する線形行列不等式条件であり、
与えられた伝達関数 ![]() が FFPR(
が FFPR(![]() )条件を 満たすかどうかの判定が、凸最適化問題を解くことにより 容易かつ厳密にできる。
)条件を 満たすかどうかの判定が、凸最適化問題を解くことにより 容易かつ厳密にできる。
![$\displaystyle \left[\begin{array}{cc} A & B \\ I & 0 \end{array}\right]^T
\lef...
...2Q \end{array}\right]\left[\begin{array}{cc} A & B \\ I & 0 \end{array}\right]$](img19.png)
![$\displaystyle \left[\begin{array}{cc} 0 & C^T \\ C & D+D^T \end{array}\right].$](img21.png)